十六进制计算器
* and,or,not,xor 运算限制为32位数字
十六进制数系统(十六进制)的功能几乎与十进制和二进制系统相同。它不是分别使用10或2的基数,而是使用16的基数。十六进制使用 16 位数字(包括 0-9),就像十进制系统一样,但也使用字母 A、B、C、D、E 和 F(相当于 a、b、c、d、e、f)来表示数字 10-15。每个十六进制数字表示 4 个二进制数字,称为半字节,这使得表示大型二进制数字更简单。例如,1010101010的二进制值可以用十六进制表示为 2AA。这有助于计算机以可以在两个系统之间轻松转换的方式压缩较大的二进制值。
以下是十六进制值、二进制值和十进制值之间的一些典型转换:
十六进制/十进制转换
| 十六进制 | 二进制 | 十进制 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 一个 | 1010 | 10 |
| B | 1011 | 11 |
| C | 1100 | 12 |
| D | 1101 | 13 |
| E | 1110 | 14 |
| F | 1111 | 15 |
| 14 | 10100 | 20 |
| 3楼 | 111111 | 63 |
在十进制和十六进制之间进行转换涉及了解不同数字系统的位置值。二进制计算器页面上提供了更深入的讨论。请注意,在十进制和十六进制之间进行转换与在十进制和二进制之间进行转换非常相似。执行任何一个转换的能力应该使另一个相对简单。如前所述,十六进制函数使用 16 的基数。这意味着对于值 2AA,每个位置值表示 16 的幂。从右边开始,第一个“A”代表“一”位置,即160。右边的第二个“A”代表161,2代表162。请记住,十六进制中的“A”相当于十进制中的10。知道了这些信息,就可以从十六进制转换为十进制,如下所示:
|
||||||
从十进制到十六进制的转换稍微复杂一些,但使用相同的概念。请参阅以下步骤和示例。请务必结合列出的步骤完成提供的示例,以便了解该过程:
- 找到小于或等于要转换的数字的 16 的最大幂,这将称为 X。
- 确定在步骤 1 中找到的 16 的幂进入 X 的次数,并记下该数字。
-
将步骤 2 中找到的数字乘以 16 的幂,然后从 X 中减去此值。此新值将称为 Y。
- 请注意,在步骤 2 中找到的数字将是写入找到的 16 次幂的位置值中的值。例如,如果发现 16 的最大幂为 164,并且步骤 2 中的数字为 3,则十六进制值的 164 位值中将具有数字 3:3qrst,其中 qrst 表示 160 到 3 位值。
- 使用 Y 作为新的起始值重复步骤 1-3。继续该过程,直到 16 大于剩余值,并将剩余部分分配给 160 位值。
- 将步骤 2 的每次迭代中找到的每个值分配给其各自的位置值,以确定十六进制值。
| EX: | 十进制 1500 转化为16进制 | |
| (1) | 最大平方数 = 162 = 256 | |
| (2) | 256 × 5 = 1280, so (5 × 162) | |
| (3) | 1500 - 1280 = 220 | |
| (4) | 16 × 13 = 208, so (13 × 161) | |
| (5) | 220 - 208 = 12 | |
| (6) | 16 比 12大, 因此 12 是 160 位置值中的值 | |
| (7) | 1500 = (5 × 162) + (13 × 161) + (12 × 160) | |
| (8) | 10-15 有字母数字 十六进制:13 = D,12 = C | |
| (9) | 因此,1500 的十六进制值为:5DC | |
从十六进制到十进制的转换使用相同的原理,但可以说更简单。将十六进制值中的每个数字乘以其相应的位置值,然后找到每个结果的总和。无论十六进制值是否包含字母数字,该过程都是相同的。
| EX: | 将十六进制 1024转为十进制 | |
| (1) | (1 × 163) + (0 × 162) + (2 × 161) + (4 × 160) | |
| (2) | 4096 + 0 + 32 + 4 = 4132 | |
十六进制加法
十六进制加法遵循与十进制加法相同的规则,唯一的区别是加法数字 A、B、C、D、E 和 F。如果 A 到 F 的十进制等效值尚未提交到内存,则在执行十六进制运算时,将 A 到 F 的十进制等效值放在手边可能很方便。下面是十六进制加法的示例。请仔细阅读该示例,并参阅其下面的文本以获取更多详细信息。
前任:| 18 | 1A | B | ||
| + | B | 7 | 8 | |
| = | 1 | 4 | 2 | 3 |
十六进制加法涉及计算基本的十进制加法,同时在存在大于 9(数字 A 到 F)的值时在十六进制和十进制之间进行转换。在上面的示例中,十进制的 B + 8 是 11 + 8 = 19。十进制 19 是 13十六进制,因为有 1 组 16,剩下 3 个。就像十进制加法一样,1 会延续到下一列。因此,下一列计算出的是 1 + A (10) + 7 = 18十进制,或 12十六进制。将 1 转到最后一列,得到 1 + 8 + B (11) = 20位十进制或 14个十六进制。这将产生 1423十六进制的结果。
十六进制减法
十六进制减法的计算方式与十六进制加法大致相同;通过在十六进制值和十进制值之间转换时执行操作。十六进制和十进制减法之间最显着的区别涉及借用。在十六进制中借用时,借用的“1”表示十进制的 16 位,而不是十进制数点数的 10 位。这是因为从中借用的列比借用列大 16 倍(与十进制中借用的 1 表示 10 的原因相同)。只要注意到这一点,并且仔细完成字母数字A-F的转换,十六进制减法并不比十进制减法更困难。请仔细阅读该示例,并参阅其下面的文本以获取更多详细信息。
前任:
|
|||||||||||||||||||||
在上面的示例右侧的第一列中,C 或 12位小数小于 F 或 15位十进制。因此,有必要从下一列借用。这会将 D 减少到 C,并将 1 或 16个小数借出到第一列。16位十进制 + 12位十进制 - 15位十进制 = 13位十进制,或第一列中的 D。以下列不需要借用,使计算变得简单。由于借用了 1,因此 C - A = 12十进制 - 10十进制 = 2,5 - 3 = 2,产生 22D 的最终结果。在被减去的数字大于被减去的数字的情况下,只需更改数字的位置,计算减法,并在结果中添加一个负号。如果上面的示例改为 3AF - 5DC,则将按原样编写,但解决方案将是 -22D。
十六进制乘法
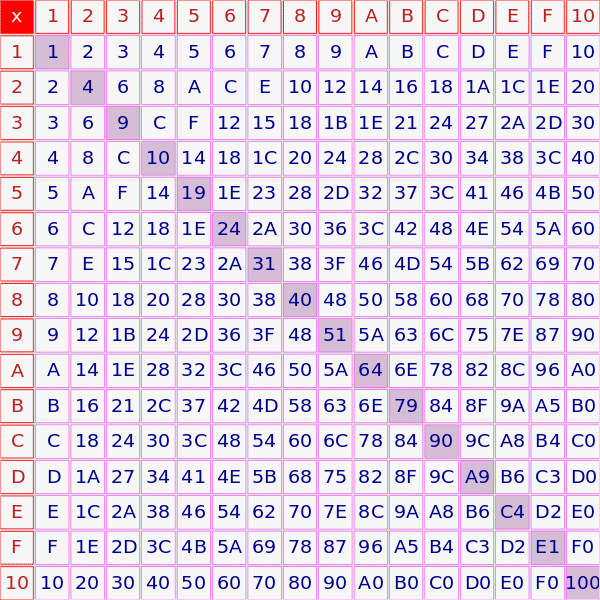
十六进制乘法可能很棘手,因为执行操作时十六进制和十进制之间的转换需要更多的努力,因为数字往往更大。有一个十六进制乘法表可能会有所帮助(下面提供了一个)。否则,每个步骤都需要在十进制和十六进制之间进行手动转换。下面是十六进制乘法的示例。在示例的右侧,显示了每个乘法和加法步骤。请注意,所有使用的数字都是十六进制。如有必要,请参阅添加部分。
EX:| F | A | 3 × A = 1E; 1 carried to F | |||
| × | C | 3 | 3 × F = 2D, + 1 = 2E | ||
| 2 | E | E | C × A = 78; 7 carried to F | ||
| + | B | B | 8 | 0 | C × F = B4, + 7 = BB |
| = | B | E | 6 | E | |
十六进制部门
十六进制中的长除法与十进制中的长除法相同,只是乘法和减法发生在十六进制中。也可以转换为十进制并以十进制执行长除法,然后在完成后转换回来。为了便于说明,除法示例将完全以十六进制计算。与乘法一样,在进行十六进制除法时,使用十六进制乘法表(下面提供了一个)会很方便。下面是一个示例。请注意,示例中的所有数字都是十六进制。尽管下面的示例中没有发生借用,但请记住,以十六进制形式借用会导致借用 16位小数,而不是 10位小数。有关更多详细信息,请参阅十六进制减法部分。

十六进制乘法表